Bei der Arbeit mit Deinem RevPi-System wirst Du immer wieder mit verschiedenen Zahlensystem konfrontiert werden. Für alle, die neu im Thema sind und für diejenigen unter Euch, die das irgendwann gelernt und wieder verdrängt haben, haben wir hier eine kleine Zusammenfassung erstellt.
Binäres Zahlensystem
Das Binäre Zahlensystem ist Grundlage für die elektronische Datenverarbeitung, da man hier nur zwischen 2 logischen Zuständen (1 und 0) unterscheiden kann. Ein Computer muss deshalb alle Berechnungen mit diesen beiden Zahlen vornehmen.
Das sieht auf den ersten Blick aus, als hätte man sehr begrenzte Möglichkeiten sich mit diesem Zahlensystem auszudrücken. Wir haben jedoch, wie in allen anderen Zahlensystemen, auch hier Stellen zur Verfügung, die Werte annehmen. Das binäre Zahlensystem basiert auf der Zahl 2. Das bedeutend, dass sich die Werte hier einfach verdoppeln:
| … | 8 | 4 | 2 | 1 |
| … | 23 | 22 | 21 | 20 |
Jede dieser Stellen kann zwei verschiedene Werte annehmen (0 oder 1). Eine einstellige duale Zahl heißt ein Bit (binary digit). Mit einem Bit lassen sich also zwei Zahlen darstellen (0 oder 1). Mit 2 Bits verdoppeln sich die Möglichkeiten:
00, 01, 10, 11
Beispiel :
Wir rechnen die Dezimalzahl 19 ins duale Zahlensystem um:
- Schreibe eine Tabelle auf, die von der Einer-Stelle des dualen Systems bis zu der Stelle geht, die noch kleiner (oder genauso groß) als 19 ist.
| 16 | 8 | 4 | 2 | 1 |
- Schreibe eine 1 unter den größten Wert, der in die 19 hineinpasst.
| 16 | 8 | 4 | 2 | 1 |
| 1 |
- Subtrahiere 16 von 19. Du erhältst den Restwert 3.
- Schreibe eine 1 unter den größten Wert, der in die 3 hineinpasst.
| 16 | 8 | 4 | 2 | 1 |
| 1 | 1 |
- Subtrahiere 2 von 3. Du erhältst den Restwert 1.
| 16 | 8 | 4 | 2 | 1 |
| 1 | 1 | 1 |
- Subtrahiere 1 von 1. Du erhältst den Restwert 0. Fülle die leeren Felder der Tabelle mit 0 auf.
| 16 | 8 | 4 | 2 | 1 |
| 1 | 0 | 0 | 1 | 1 |
Die Dezimalzahl 19 entspricht der Dualzahl 10011.
Hexadezimales Zahlensystem
Das hexadezimale Zahlensystem wird verwendet, um große Dualzahlen übersichtlich darzustellen. Lange Bitfolgen werden hier in jeweils 4 Bit aufgeteilt und in eine hexadezimale Zahl umgerechnet.
Beispiel:
| Bitfolge | 010100001100101000111111 | |||||
| gruppierte Bitfolge | 0101 | 0000 | 1100 | 1010 | 0011 | 1111 |
| Umwandlung in Hexzahlen | 5 | 0 | C | A | 3 | F |
| gruppierte Hexzahlen | 50 | CA | 3F | |||
Übersicht der Zahlensysteme
| Nummer | Hexadezimal | Dezimal | Binär/Dual | ||||
| Stelle | 1 | 2 | 1 | 4 | 3 | 2 | 1 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 2 | 1 | 1 | 0 | 0 | 0 | 1 | |
| 3 | 2 | 2 | 0 | 0 | 1 | 0 | |
| 4 | 3 | 3 | 0 | 0 | 1 | 1 | |
| 5 | 4 | 4 | 0 | 1 | 0 | 0 | |
| 6 | 5 | 5 | 0 | 1 | 0 | 1 | |
| 7 | 6 | 6 | 0 | 1 | 1 | 0 | |
| 8 | 7 | 7 | 0 | 1 | 1 | 1 | |
| 9 | 8 | 8 | 1 | 0 | 0 | 0 | |
| 10 | 9 | 9 | 1 | 0 | 0 | 1 | |
| 11 | A | 1 | 0 | 1 | 0 | 1 | 0 |
| 12 | B | 1 | 1 | 1 | 0 | 1 | 1 |
| 13 | C | 1 | 2 | 1 | 1 | 0 | 0 |
| 14 | D | 1 | 3 | 1 | 1 | 0 | 1 |
| 15 | E | 1 | 4 | 1 | 1 | 1 | 0 |
| 16 | F | 1 | 5 | 1 | 1 | 1 | 1 |
Machs Dir nicht so schwer!
Kopfrechnen hält Dich zwar geistig fit, aber falls es doch mal schnell gehen soll, geht’s auch mit dem Zubehör-Rechner auf Deinem PC:
- Öffne den Zubehör-Rechner.
- Wechsle in die Programmierer-Ansicht.
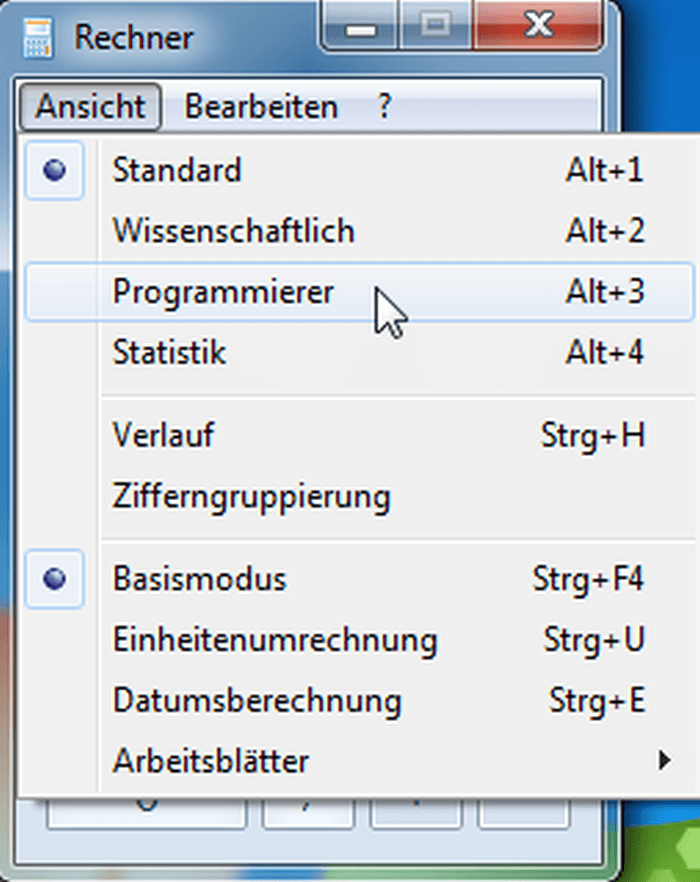
- Gib einen Wert ein.
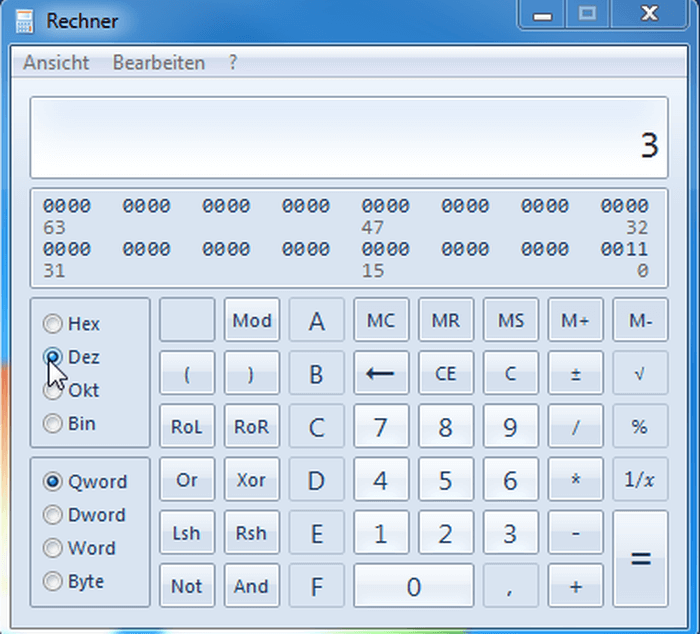
- Wähle das gewünschte Zahlensystem aus.
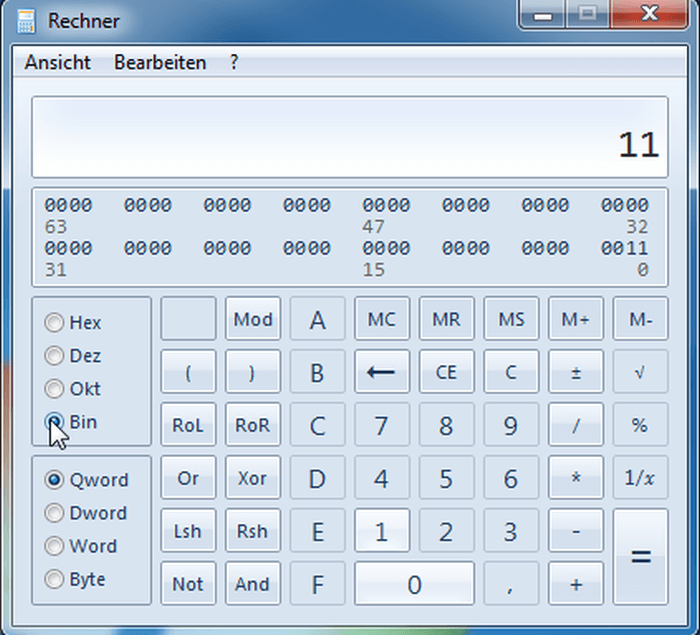
Der Wert wird Dir im gewünschten Zahlensystem angezeigt.
